Перевод брошюры Как читать MTF-графики на русский язык осуществлён Николаем Мыльниковым. За что ему большое спасибо!

How to Read MTF Curves

By H. H. Nasse
Carl Zeiss Camera Lens Division December 2008
Скачать брошюру Как читать MTF-графики. Брошюра от Carl Zeiss на английском
[lock][download id=43][/lock]

Как читать кривые MTF

Предисловие

Из интернетовской дискуссии «Как читать кривые MTF» был сделан хороший честный вывод, показывающий нам, как трудно фотографам понять этот мир цифр. Тем не менее, на последующих страницах будет показано, что дело не так и плохо, и вполне возможно представить основные закономерности без экскурсии в высшую математику оптики Фурье. После прочтения этой статьи вы сможете делать заключения о характеристиках объективов на основании данных MTF, публикуемых производителями или тестирующими институтами. Вместе с тем, вы поймете пределы использования MTF, и это позволит вам критически относиться к обзорам объективов. А те, кто мало обращает внимания на цифры и графики могут утвердиться в своей уверенности, что для хорошего фотографа это действительно не нужно, т.к. фотография основывается, гл. обр. на опыте. Но есть люди, желающие лучше понимать работу своих инструментов, и именно этого они смогут достичь при чтении этой первой части. Во второй – мы покажем вам несколько иллюстраций.

Функция рассеяния точки

Когда фотограф намеревается получить точное соответствие снимка объекту он должен пожелать получить на свою камеру идеальный объектив, тот, что позволяет всем лучам света, исходящим из одной точки объекта снова в точности сойтись в одной точке снимка. Сейчас мы знаем, что с реальными объективами мы прошли лишь часть пути для достижения идеала. Точка изображения, в геометрическом смысле слова, в действительности не существует. Абберации в системе линз объектива, производственные допуски, волновая природа света, в конечном счете, приводят к тому, что свет, исходящий из одной точки объекта всегда распределяется по области, лежащей вокруг идеальной точки изображения. До определенной степени, эта область является «минимально возможной окружностью возмущения». Однако вокруг области свет распределяется неодинаково, и его интенсивность снижается от центра к краям, а форма редко бывает округлой. Этот эффект известен как «Функция рассеяния точки» (point spread function). Её форма и размеры характеризуют качество изображения объектива. Если возможно сравнить фотографию с полотном, то функция рассеяния точки будет мазком. Подобно тому, как кисти бывают широкие, узкие, точечные или даже лохматые, объективы тоже имеют различные «стили письма».

Тогда почему до сих пор не используются количественные методы описания качества изображения? Для этого имеются три причины:
1. Форма области иногда очень сложная и не поддается простому количественному описанию. Это показано на следующих картинках, полученных с помощью микроскопа. Первые шесть точек, показанных на следующей странице, являются примером реальных, но средних по качеству изображений, типичных для светосильных объективов на полной диафрагме, широкоугольных объективов на краю изображений или объективов слегка расфокусированных. Маленькие белые квадратики в каждом изображении помещены для сравнения и представляют 8,5 мкм пиксель, подобный тому, что находится на 12 МР полнокадровой матрице 35 мм камеры. Все эти области рассеяния точки, как можно видеть, значительно больше, чем площадь (относительно большая) пикселя.

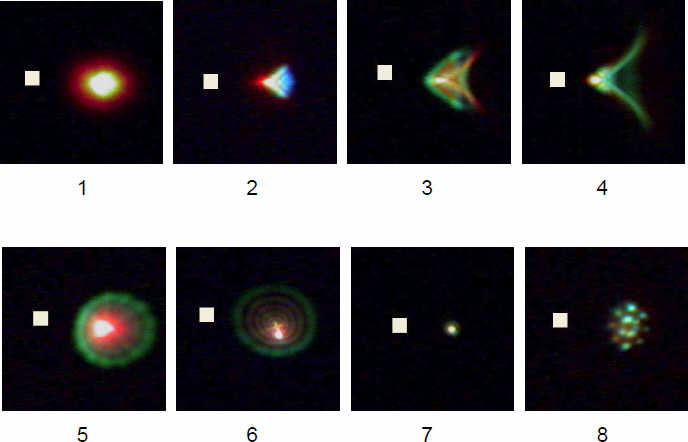
Рассеяние точки №7 – пример выдающегося качества изображения. Однако цифровой сенсор обычно не видит такое маленькое рассеяние точки. На изображении №8 показано то же самое рассеяние помещенное за низкочастотный (low pass) фильтр, к-рый обычно помещают перед сенсором для подавления муара. Качество изображения, таким образом, намеренно ухудшают, значительно увеличивая рассеяние точки при помощи нескольких дисков с двойным лучепреломлением.
2. Вы почти никогда не увидите такое одиночное, изолированное точечное рассеяние. Только сфотографировав звезду темной ночью, можно достичь эффекта, приведенного здесь и полученного в лаборатории. Большинство изображений создаются в камере путем сложной комбинации частей большого количества единичных рассеяний точек. Т.к. небольшой участок объекта состоит из многих близко стоящих точек, что соответствует многим плотно стоящим идеальным точкам изображения, получаемым позади объектива. Поскольку реальные рассеяния точек не могут быть бесконечно малыми, то это означает, что индивидуальные рассеяния точек перекрываются. Интенсивность единичной точки изображения (можно даже сказать единичного пикселя) создаются взаимодействием (сложением) многих рассеяний точек. Т.е. являются математически трудно описуемой связью между «мазком кистью» и изображением, которое мы видим.
3. Состоит в том, что целостная воображаемая цепь от объектива до глаза может быть более просто описана с помощью метода, который я собираюсь сейчас объяснить.

Воспроизведение модуляции (Modulation transfer)

Поскольку в первую очередь нас интересует получение изображений протяженных объектов, объектов не похожих на звезду и состоящих из неопределенного числа точек, то нам необходимо найти другой способ количественного описания качества изображения. Для того, чтобы изучить как выглядит простой, насколько это возможно, объект на изображении мы используем синусоидальное распределение яркости. Синусоидальное распределение яркости – это последовательность светлых и темных полос, между которыми переход между яркостью и темнотой происходит постоянно и постепенно, т.е. синусоидально. Синусоидальный полосатый образец используется потому, что получаемое изображение, неизменно, тоже является синусоидальным, независимо от того, каким бы сложным ни было рассеяние точки. Некоторые его свойства остаются неизменными, или, по крайней мере, не оказывают влияния на качество изображения: не изменяются направление полосок и их частота, т.е. количество на единицу длины. Эти показатели изменяются только с изменением образца. Что не идентично более оригиналу, так это различие в яркости между светлыми и темными полосками. Это происходит потому, что из-за протяженного рассеяния точки часть света не попадает на яркие полоски, а попадает на области, которые в действительности должны быть абсолютно черными.

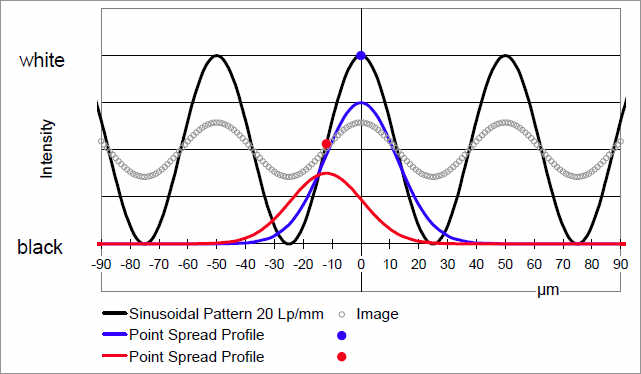
На приведенном графике показан синусоидальный профиль яркостей последовательности темных и светлых полос (черная кривая) в виде профиля интенсивности (сечение перпендикулярное направлению полос). На один миллиметр приходится 20 периодов, т.е. 1 период равен 50 микрометрам (мкм). Красная и синяя кривые – поперечные сечения распределения яркостей в рассеяниях точек. Яркость точки, лежащей на кривой и обозначенной синим, которая отобразится на идеальном изображении, распределится на окружающей поверхности в соответствии с синей кривой. Видно, что часть света подает в темные «долины» на 25 мкм отстоящие от синей точки. Свет также падает сюда и от точки кривой, обозначенной красным цветом. Хотя красная точка лежит на боку кривой и, следовательно, темнее, значительная часть света достигает точки -25мкм т.к. красная точка ближе к темной «долине». Т.о. освещенность темных областей образца является суммой добавочного света, поступающего с соседних участков. В результате изображение будет характеризоваться кривой с ослабленной модуляцией (помеченной «image»). Яркость темных полос изображения возрастает из-за отклонения света, а яркие полосы становятся темнее. В оптике различия между ярким и темным определяется как контраст. С более общей точки зрения, различия между максимальным и минимальным значениями, для любого синусоидального периодически изменяющегося показателя называется «модуляция». Если мы сравним модуляцию объекта с модуляцией изображения, просто разделив эти цифры одна на другую, мы получим число, характеризующее изобразительные свойства объектива: воспроизведение модуляции (modulation transfer). Т.о. мы уже понимаем, что обозначают первые две буквы в термине «MTF». Это число от 0 до 1 или от 0% до 100%. Фотографы для отражения различий между светом и тенью используют шаги диафрагмы, которые отражают логарифмическую шкалу чувствительности наших глаз. Но, для примера, что означает воспроизведение модуляции 50%, если различия между темными и светлыми точками нашего образца составляют 6 шагов диафрагмы? Не означает ли это, что соотношение яркостей составляет 1:26 = 1:64? Может быть, различия между яркостями в изображении составляют 3 шага диафрагмы, или м.б. 1:32, т.е. 5 шагов диафрагмы? И то и другое неверно. В действительности в этом случае мы имеем примерно 1,5 шага диафрагмы. Это потому, что в оптике параметр «контраст» определяется следующим образом:

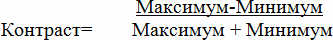
Поэтому в нашем случае контраст объекта приблизительно 0,97 (63:65). После получения изображения с воспроизведением модуляции (modulation transfer) 50% контраст снизился в 2 раза, приблизительно до 0,48. Минимум и максимум, т.о составили 1:2,9 (1,9/3,9 = 0,48). Следующий график показывает как контраст объекта и контраст изображения связаны для различных воспроизведений модуляции (modulation transfers) если измерять их в шагах диафрагмы.

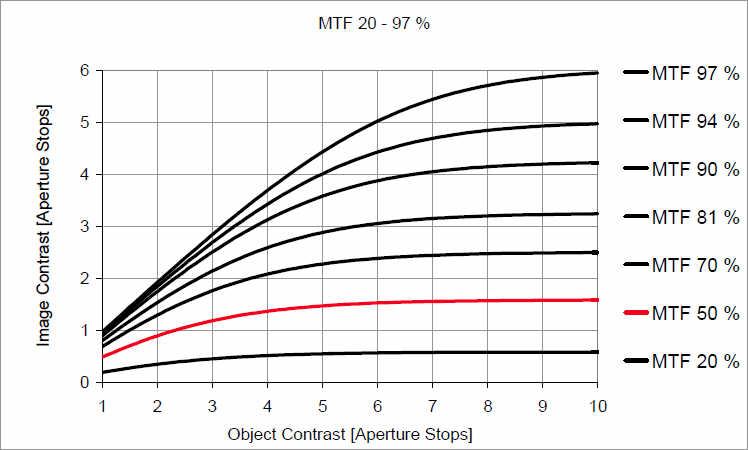
График демонстрирует 3 важных свойства MTF, которые мы должны помнить, изучая кривые MTF:
1. Небольшие различия между высокими показателями MTF становятся особенно заметными при высоком контрасте объекта.
2. С другой стороны, слабая изменчивость в тонах – менее одного шага диафрагмы – не требует высоких значений MTF. Различия более 70-80% вполне уместны.
3. При очень низких значениях MTF контраст объекта практически не имеет значения. Контраст изображения будет всегда низким.
Именно поэтому в спецификации пленки всегда также указывается разрешение при низком контрасте 1:1,6. Контраст в 1:1000 может быть измерен только методом контактной экспозиции. Ни один объектив в мире не способен передать изображение очень мелких структур (например, очень высокую частоту полос) с контрастом в 10 шагов диафрагмы. Желание получить на пленке такое высокое разрешение, т.о., слишком оптимистично.

Функция воспроизведения модуляции (modulation transfer function)(MTF), разрешающая способность (resolving power)

Очевидно, что образец, состоящий из одной полоски недостаточен для характеристики объектива. Образец с широкими промежутками м-ду светлыми и темными полосками, конечно, может быть хорошо воспроизведен объективом с большой областью рассеяния точки. Если же мы уменьшим расстояние м-ду полосками до такой степени, что оно приближается к величине функции рассеяния точки, то часть света ярких зон будет попадать на темные и контраст изображения сильно упадет. Продолжая сравнение с кистями, можно сказать, что крупные структуры можно изобразить толстой кистью, для изображения же тонких деталей требуется тонкая точечная кисть. Т.о. нам требуется исследовать, как объектив передает изображения образов с различной толщиной полос, т.е. мы должны определить воспроизведение частот (modulation transfer — МТ) для каждого из этих образцов. При этом мы получаем целостную последовательность чисел и если затем мы представим их в виде функции, описывающей толщину линий образца, то последовательность этих чисел будет представлять кривую, называемую функцией воспроизведения колебаний (modulation transfer function) – MTF.
Толщину полос можно измерять, подсчитывая их кол-во (периодов: белый-черный) на 1 мм изображения. Период – это расстояние между двумя яркими или двумя темными полосками, ширина пары линий состоящей из одной яркой и одной темной. Кол-во периодов в 1 мм на плоскости изображения – частота полос. Она характеризуется показателем пара линий на 1 мм, сокращенно л/мм (lp/mm).

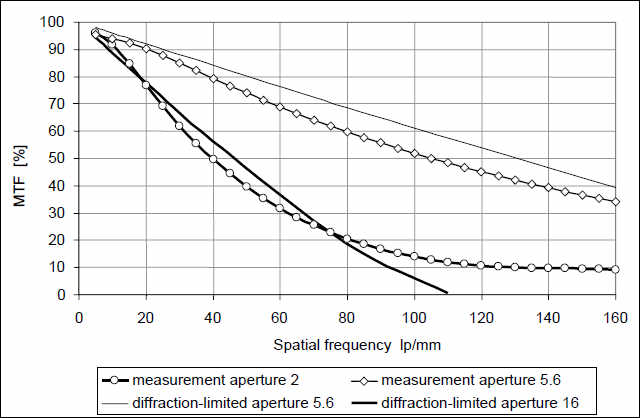
MTF 50 мм объектива в 35 мм формате в центре изображения, измеренная при диафрагме 2 и диафрагме 5,6 для сравнения. Так же приводится воспроизведение модуляции ограниченное дифракцией для диафрагмы 5,6 и диафрагмы 16 (сплошная линия без кружков). Самая лучшая картинка – ограниченная только дифракцией. По горизонтальной оси отложена частота пар линий на мм.

Если изображение ограничено только явлением дифракции, то MTF представляет почти прямую линию, снижающуюся пропорционально возрастанию частоты полос. MTF = 0 достигается при этом в т.н. точке предела частоты полос, которая определяется диафрагменным числом и длиной волны света. Приближенно можно считать, что для средней длины волны видимого света ширина области рассеяния точки в мкм соответствует диафрагменному числу, а предельная частота полос приблизительно равна 1500, деленное на диафрагменное число.

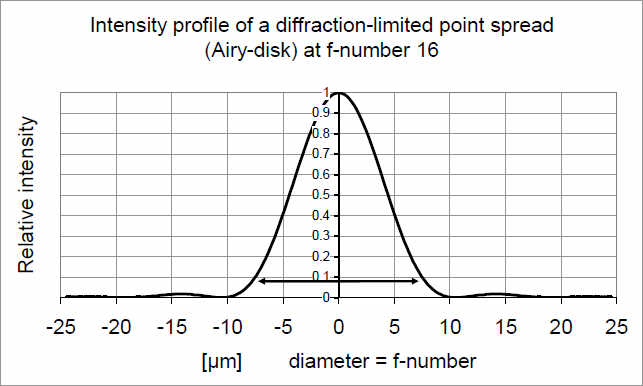
У реальных объективов, имеющих остаточные абберации, значения MTF сначала быстро снижаются, а затем очень медленно приближаются к 0. Т.е кривая явно провисает. В вышеприведенном примере это явно наблюдается для кривой апертуры 2; при диафрагме 5,6 характеристика объектива не слишком отличается от физически возможного оптимума. Частота линий, при которой значение MTF достигает 0, или опускается ниже предельного порога (н-р 10%) называют разрешающей способностью объектива в воздухе. Образцы с чередующимися полосами могут содержать всё более тонкие линии, прежде, чем их изображение сделается сплошным серым. Кривая для диафрагмы 2, в частности, показывает, что предел разрешения здесь трудно измерить. Очень слабый наклон кривой при высоком значении частоты полос означает, что результат определяется минимумом требуемого контраста. Измерения поэтому очень неточны. Исходя из этого, оказывается, что недостаточно характеризовать объектив только разрешающей способностью. И уж совсем не следует путать этот показатель с разрешающей способностью, достигаемой при взаимодействии объектива и сенсора. Это снова возвращает нас к 3-ей причине, по которой мы описываем качество изображения с помощью MTF: мы никогда не воспринимаем изображение, получаемое объективом непосредственно глазами, всегда требуется еще одно звено в цепи формирования изображения, Мы всегда нуждаемся в приемнике изображения: сенсоре – цифровом или аналоговом, или сканере, принтере, или проецирующем устройстве. Каждый из этих компонентов, наряду с глазом человека имеет свои изобразительные св-ва, каждое из к-рых м.б. описано функцией воспроизведения. И хорошие показатели MTF, как MTF целостной цепочки формирования изображения является продуктом всех индивидуальных MTF.

Рассмотрим несколько типичных примеров:

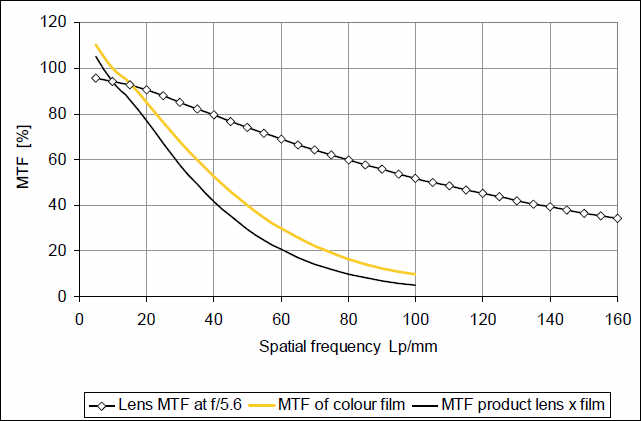
Две MTF: очень хорошего 35-мм форматного объектива и цветной негативной пленки. Результат всегда слабее, чем самый слабый фактор в цепи формирования изображения. В данном случае, общее качество изображения существенно ограничено свойствами пленки. Если принять минимальное воспроизведение модуляции в 10%, то разрешающую способность следует ожидать на уровне 80-100 л/мм. Если принимать во внимание наличие других элементов — глаз или оптика проектора – результат будет существенно хуже.

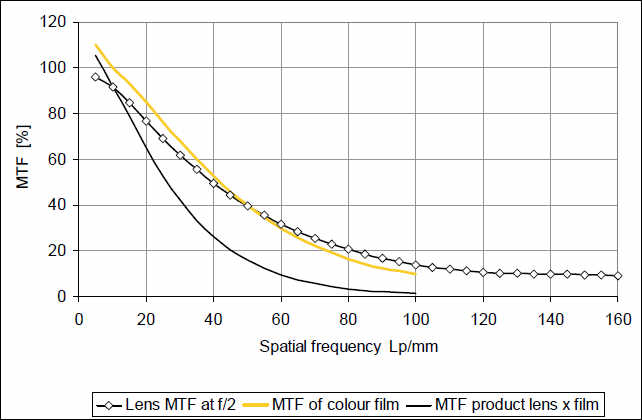
Результат сложения двух функций воспроизведения модуляции: 35-мм объектив среднего качества и цветной негативной пленки. В этом случае, суммарная кривая почти в равной степени определяется св-вами объектива и пленки.

Если рассматривать кривую образованную только двумя функциями воспроизведения, имея в виду, что в действительности этих функций может быть больше и они могут только ухудшать результат, то станет ясно, что нет необходимости использовать много образцов с очень высокой плотностью линий на 1 мм. Цифровой сенсор в 24 МП в 35мм формате, или 15 МП в APS-C формате имеют разрешение около 90 л/мм. Теоретически их разрешение можно сравнить с разрешением цветной негативной пленки. Поэтому при этих форматах обычно бывает достаточным рассматривать частотный образец до 40 л/мм. Если кол-во пикселей больше, то 40 л/мм становится более важным показателем, чем обычно.
Другое соображение в пользу того, что это достаточный предел заключается в следующем: если рассматривать изображение в формате А4 с расстояния 25 см и видя т.о. изображение под углом 60о, то глаз способен различить до 1600 линий на изображение по высоте. Т.е. его максимальное разрешение в этом случае составляет 8 л/мм. Это расстояние «наименьшая дистанция ясного видения». Для формата 35мм с 24 мм по высоте это соответствует 66 л/мм. Частота полос важная для глаза находится, т.о. тоже в пределах до 40 л/мм.
Если увеличить изображение, то с короткой дистанции будут видны более мелкие детали, и можно увидеть погрешности изображения незаметные при нормальном рассматривании изображения. Это похоже на то, когда цифровое изображение рассматривают на большом мониторе при 100% увеличении. Изображение в 12 МП при этом будет более 1 м в ширину. Сенсор способный воспроизводить разрешение обеспечиваемое объективом – это низкочувствительная черно-белая пленка.

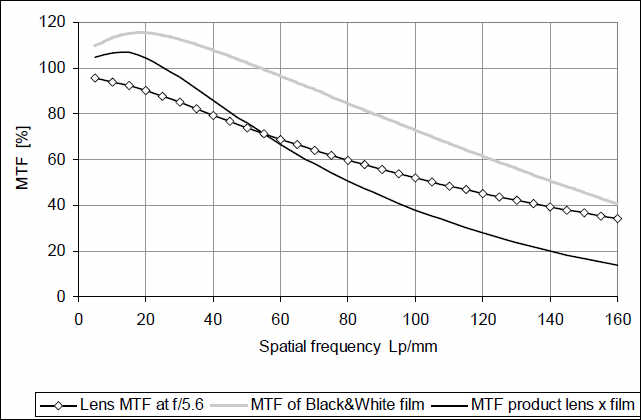
Хороший объектив в сочетании с черно-белой пленкой высокого разрешения (Из Т-Мах-100)

На следующей картинке графически показано, что 40 л/мм достаточно высокая частота, по крайней мере, для 35мм формата. Это хорошо известные звезды Сименса, часто используемые для испытания камер. Полная картинка для 12 МП камеры в 35мм формате содержит 9 звезд.

Сильно увеличенное изображение центра звезды Сименса показывает, как близко к центру располагаются линии, частота которых 40 л/мм.

Определение границ, контраст изображения

Мы уже знаем почему модуляция синусоидального полосатого образца на оптическом изображении понижается по мере увеличения частоты полос, а также на дальнейших стадиях образования изображения вплоть до его восприятия. Но что могут сказать нам эти цифры о качестве реальной картинки? Каковы отношения между такими терминами как: четкость, яркость, разрешение деталей etc. и этими числами? Наш объект съемки, конечно, не содержит синусоидальных деталей. Они могут быть приблизительно созданы только в условиях лаборатории, поэтому используются другие тест-объекты, по которым синусоидальная модуляция рассчитывается математически. В специальных тестах для оценки объективов и камер и определения эффективной разрешающей способности используются образцы с прямоугольным профилем интенсивности, резким переходом между черным и белым. Передача модуляции для прямоугольного образца, обычно несколько лучше, чем для синусоидального той же частоты. Однако такие резко прямоугольные формы тоже редко встречаются в реальной фотографии. Тонкие периодические структуры, которые наш глаз использует для оценки качества картинки, присутствуют лишь на небольших фрагментах снимка. На самом деле наиболее важными являются переходы, границы между двумя областями, различающимися по яркости или цвету. Хотелось бы понять каковы взаимоотношения между MTF и воспроизводством переходов. Это опять приводит нас к функции рассеяния точки.
Ниже, слева направо представлены рисунки:
1. Профиль интенсивности функции рассеяния точки в логарифмической шкале вплоть до 1/1000 от максимальной интенсивности, находящейся в центре. Ширина функции рассеяния точки представлена в мкм, 1 мкм = 1/1000 мм.
2. Профиль интенсивности двух границ в изображении с большим и малым переходами яркостей. Вертикальная шкала – логарифмическая шкала диафрагм знакомая фотографам. Каждое деление отражает имеющуюся освещенность. Горизонтальная шкала – опять же мера расстояния на изображении в мкм. Яркая и темная стороны перехода находятся, соответственно, слева и справа.
3. Воспроизведение модуляции для 5 частотных образцов: 5, 10, 20, 40 и 80 л/мм представлено в виде столбиков на соответствующей диаграмме.

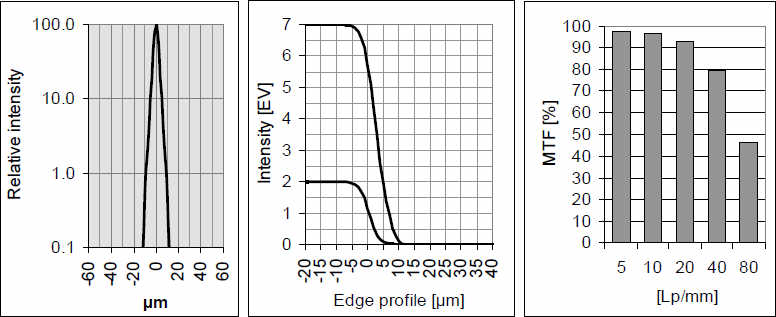
Пример очень хорошего изображения в 35 мм формате: рассеяние точки узкое, переход между белым и черным узкий – не шире 10 мкм, т.е. очень крутой. Фотографы говорят в таких случаях: границы резкие. На языке передачи модуляции на такие характеристики указывает тот факт, что показатели воспроизведения всех частот очень высокие и не сильно снижаются при возрастании частот. Для объективов с такими параметрами изображения качество получаемой картинки ограничивается обычно свойствами сенсора, аккуратностью фокусировки, движением камеры etc.

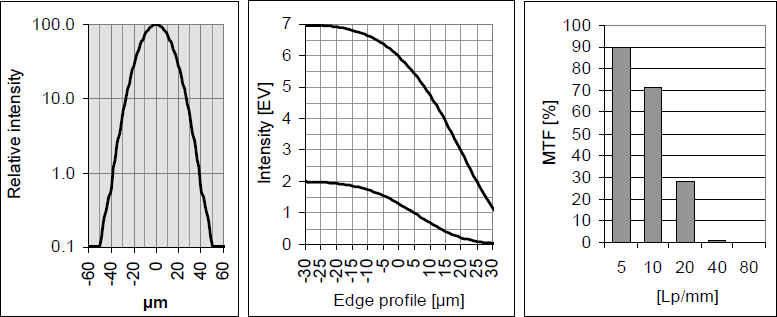
Если диаметр функции рассеяния точки значительно больше, то изображение переходов от белого к черному не назовешь резким. Профиль границы плоский, т.к. переход от максимальной яркости к черному составляет 30-50 мкм в зависимости от величины изменения яркостей. Тем не менее, абсолютно черный на этом изображении присутствует и контраст м-ду вершинами и концами кривых высокий. Значения MTF быстро падают с возрастанием частоты образца, что объясняет предшествующие показатели. При 10 л/мм MTF незначительно отличается от предыдущего примера (высокий контраст).

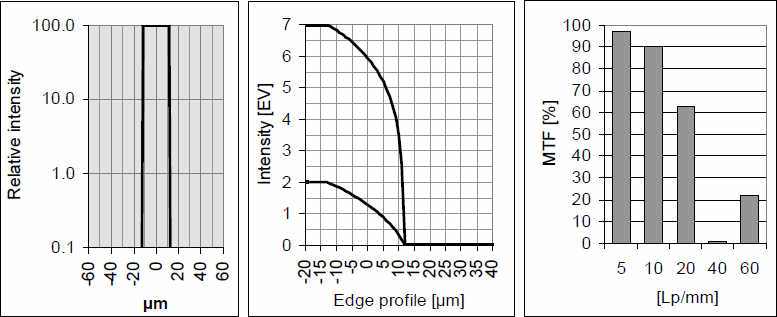
Профиль рассеяния точки в виде прямоугольника естественным образом приводит к ослаблению способности видеть границу. Показатели MTF на низких и средних – до 20 л/мм — частотах нормальные. Даже при 60л/мм воспроизведение модуляции остается на приемлемом уровне. Если учитывать только эти значения частот, то можно думать, что изображение будет вполне приличным.
Но: здесь нет контраста при 40 л/мм! Кривая воспроизведения модуляции может упасть до 0, а затем вновь подняться. Такое явление называется «фальшивым разрешением», что не совсем удачно, поскольку структуры с частотой 60 л/мм заметно воспроизводятся. Обычно остается незаметным, что черное и белое меняются местами (за исключением звезды Сименса) и следующая точка 0 придется на частоту 80 л/мм, затем изображение вновь появится с черным и белым на своих местах. Термин «фальшивое разрешение» подчеркивает, что отдельная демонстрация высокого разрешения в одной особо предпочитаемой частоте может создавать впечатление высокого качества картинки, которое в действительности отсутствует. В публикуемых MTF вы не найдете такого рода изображений, но в практике они имеют место и приводят к ошибкам фокусировки и блюру, вызываемому движением.

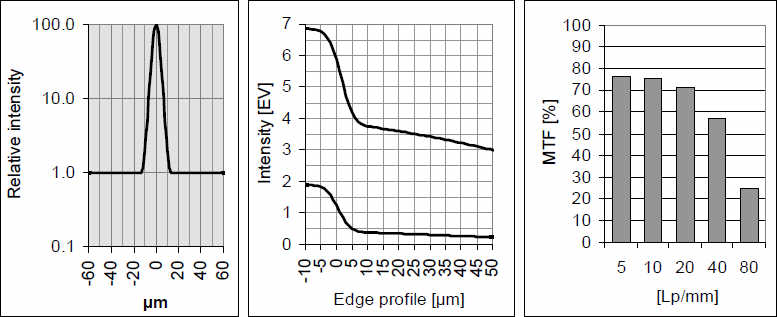
Следующая функция рассеяния точки такая же узкая, как и в первом примере, но окружена слабым ореолом (halo). Определение границ на части графика четкое, но в тоже время широкие. Яркие лучи протягиваются в зону темноты. Фотограф скажет, что объектив подсвечивает. Контраст между светом и тенью слабый.

Величина MTF этого четвертого типа характеризуется тем, что с повышением частоты снижается слабо, как и в 1-м случае, но при низких значениях частот: 5 и 10 л/мм невысокая. Изобразительные качества объектива с такими характеристиками могут быть до некоторой степени непостоянными и проявляться различно в зависимости от содержания изображения. Границы низкого и среднего контраста воспроизводятся с одинаковой резкостью, в частности, если выдержка короткая. Тонкие структуры со слабым контрастом становятся несколько плоскими, а границы с достаточным контрастом и света подсвечиваются или становятся более широкими при обычных выдержках.
Многие светосильные стандартные объективы 60-х годов на больших диафрагмах были откорректированы именно таким образом. При 10 л/мм они имели только 60-70% MTF, у современных объективов это значение обычно 80-90%.
Иногда говорят, что такие объективы «оптимизированы по разрешению». Это не совсем верно, т.к. они просто хорошо воспроизводят границы, а разрешающая способность для тонких периодических структур не лучше, чем у объективов с другими техническими характеристиками. Во времена доминирования черно-белой фотографии низкий контраст таких объективов можно было компенсировать, используя высококонтрастную бумагу. При цветной фотографии с ее менее гибким процессом лабораторной обработки позже требовались изменения в способах коррекции для получения нужного контраста. Впрочем такие объективы до сих пор находят своих поклонников. Поэтому следует быть осмотрительным, высказывая свое мнение об объективах. Например, знаменитый мягкий портретник 'IMAGON' имеет следующую MTF:

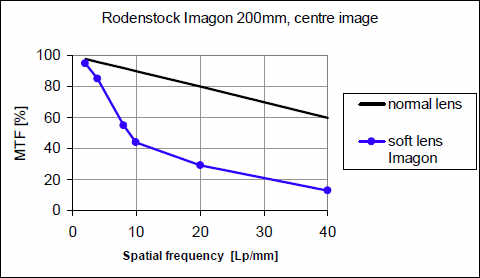
Между прочим, это не значит, что при расчете объективов приходится делать выбор между высокой разрешающей способностью и хорошим контрастом изображения: у объективов с хорошей коррекцией есть и то и другое.
Но что обозначает «контрастное изображение»? Мы не должны забывать, что когда мы говорим о «контрасте», мы всегда имеем в виду микроконтраст, т.е. структуры, которые, например, на слайде — еще видны или уже не видны невооруженным глазом. А когда мы фотографируем, например, шахматную доску, так, чтобы она полностью занимала площадь снимка, с контрастом между белыми и черными квадратами ничего не происходит. Измерения MTF ничего не говорят о таком макроконтрасте. Они оценивают только степень коррекции объектива, т.е. небольшие отклонения световых лучей, тогда как макроконтраст зависит от замутненности чистоты, непросветленности объектива, т.е. от больших отклонений. Последние – результат нежелательных отражений между оптическими поверхностями и рассеяния света на внутренних бочкообразных компонентах. Поэтому свет обычно достигает поверхности изображения более длительным путем, чем напрямую. Эти характеристики обычно смешивают между собой в термине «яркость картинки». Васокие показатели MTF при низких частотах линий необходимы, но недостаточны для получения «яркой картинки» (звенящей?).

Увеличенные изображения фрагмента шахматной доски. Слева – совершенное качество изображения; середина – слабый микроконтраст; справа – значительная степень замутненности.

Свойства изображений приведенных выше, иллюстрируют их гистограммы: у картинки, полученной объективом со слабым микроконтрастом правый пик значительно шире, чем левый, т.к. светлые тона на границах частично заходят на области черного. Тем не менее, расстояние между пиками на шкале серого точно такое же, как и для левого отличного изображения. На правой картинке с высоким уровнем замутненности пик темных тонов на гистограмме перемещен в сторону светлых, т.к. черный осветлен замутнением объектива по всему полю изображения.

Основные четыре типа функций рассеяния точки, приведенные выше, и, соответствующие им кривые MTF, можно обнаружить в характеристиках всех объективов, не всегда в виде примеров, показанных здесь, но обычно, как их комбинация. Эти примеры также показывают, что MTF следует изучать для нескольких пространственных частот. Показатель 75% для 10 л/мм будет недвусмысленным только для изображения синусоидного образца. Для реального изображения он всегда также зависит от величин показателей для 20 и 40 л/мм. Если они очень высокие, то объектив отлично прорисовывает границы, дает прекрасный контраст и хорошо передает света, как в нашем 4-ом примере. Если эти показатели ниже, то объектив теряет резкость, может быть слегка расфокусирован и у него нет «звона».
Тесты, оценивающие только одну точку MTF, например разрешение или частоту линий при к-рых MTF достигает 50% стоят немного. Это можно сравнить с оценкой HI-FI системы: я знаю, какую частоту лучше всего воспроизводят динамики или как воспроизводится частота 400Hz, но не знаю как звучит в них музыка.

Определение границ в цифровом изображении

При преобразовании реального изображения в цифровое большое значение имеет MTF камеры. Путем легкого осветления светлого края границы и притенения темного, производится подчеркивание границ. Этот прием повышает микроконтраст, резкость перехода границ и при этом субъективное восприятие резкости значительно улучшается без увеличения разрешения в деталях. Это убедительно доказывает, что четкость и разрешение не одно и то же. На MTF такие манипуляции можно обнаружить по кривой, которая частично или полностью прерывается, как это происходит у объективов, рисующих очень резкие переходы, хотя нормально должна понижаться с повышением частоты образцов.
При построении цифрового изображения можно даже усилить контрастность границ и создать функцию, которая возрастает с увеличением частоты полос. На языке теории воспроизведения она т.о. имеет характер high-pass, а такие системы способны создавать искусственные границы.

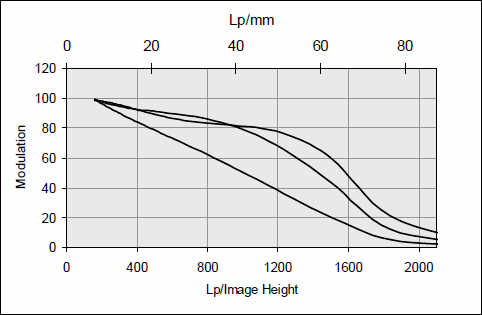
Модуляция в изображении Зеркальной 24 МП камеры 35 мм формата при различных режимах усиления переходов при внутрикамерном преобразовании в JPEG. Кривая с плоской вершиной в район 50 л/мм относится к изображению с наиболее высоким усилением границ.

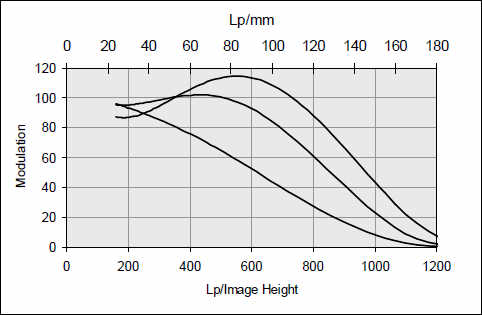
Модуляция в изображении 2/3'' камеры при минимальном, среднем и максимальном усилении границ. При горбатой кривой следует ожидать сильных артефактов. За границей темной зоны при этой кривой обычно наблюдаются дополнительные яркие линии.

Тангентальный и сагитальный

До сих пор мы рассматривали отношения между функцией воспроизведения и функцией рассеяния точки. Мы увидели, как форма функции рассеяния точки и распределение интенсивности света в ее пределах влияет на функцию воспроизведения при различных частотах полос. Здесь мы рассмотрим MTF как функцию параметров частоты полос.
Функция верна только для одной единичной точки изображения, тем не менее, даже для этой точки мы должны иметь несколько кривых, т.к. из наших примеров мы видели, что области рассеяния точки не обязательно округлые. Некоторые можно сравнить с плоской кистью, которой можно рисовать тонкие линии лишь в одном направлении. Если мы повернем частотный образец, то можем ожидать, что увидим другую MTF-кривую, которая зависит от того, короткая или длинная ось области рассеяния точки перпендикулярна направлению полосок образца.

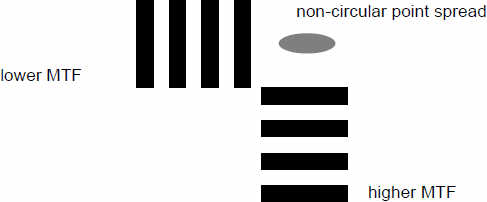
Главные направления, т.е. короткая или длинная сторона функции рассеяния точки всегда параллельна или перпендикулярна радиусу окружности изображения, т.к. объектив имеет вращательную симметрию. Образец полоски которого длинной стороной направлены к центру в оптике принято называть радиальными или сагиттальными (sagitta — лат. стрела). Это направление обычно обладает лучшим воспроизведением модуляции. Полоски перпендикулярные им ориентированы так же как касательные к окружностям, лежащим вокруг центра изображения. Такую ориентацию полосок называют тангенциальной или меридиональной.

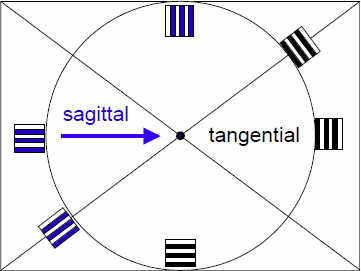
Кривые MTF для объективов

Поскольку качество изображения объективов изменяется, в общем, от центра к краям, и поскольку именно эти различия представляют для нас особый интерес, то, естественно, что для тангенциального и сагиттального направлений нам требуется больше, чем 2 кривые. Для описания частотных изменений свойств изображения с удовлетворительной точностью между центром и углом требуется полдюжины или около того точек измерения. Это будет в целом 12 кривых – не слишком ясная и четкая картина.
Кривые MTF, которые мы уже хорошо знаем, и для построения которых на вертикальной оси мы откладываем воспроизведение модуляции, а на горизонтальную – частоту полос, на самом деле удобны только для сенсоров, т.к. его характеристики не изменяются по площади. Для объективов такое представление результатов неудобно. Поскольку кривая MTF, являясь функцией частоты полос, всегда более или менее быстро падает вправо, становится достаточным выделить 3 различных значения для каждой кривой, обычно это 10, 20 и 40 л/мм. Если показать как кривые MTF для этих частот изменяются по площади изображения, то мы получим графики более удобные для объективов.
Именно поэтому на кривых MTF, приводимых в наших данных, воспроизведение модуляции приводится на Y-оси, а высота изображения – сечение оптической оси – на X-оси. На диаграмме показано 6 кривых, т.е. тангенциальная (прерывистая линия ) и сагитальная (непрерывная линия) для каждой из 3 частот. Верхняя из 6-ти кривая всегда относится к само низкой частоте, а нижняя, конечно, к самой высокой.

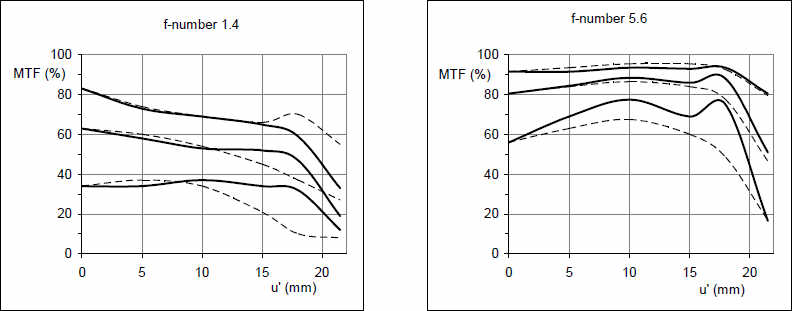
Кривая MTF объектива Planar 1.4/50 ZF для 10, 20 и 40 л/мм; белый свет, фокусировка на бесконечность

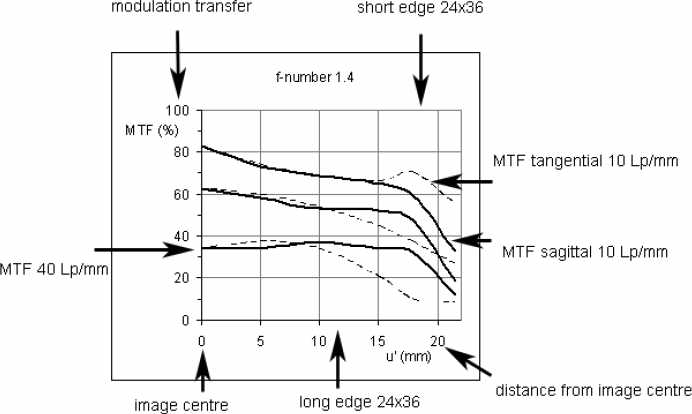
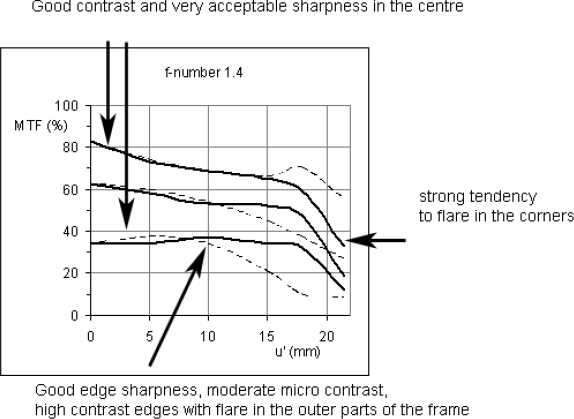
В центре этот объектив достигает при 10 л/мм более чем 80% MTF даже при полностью открытой диафрагме, но при 40л/мм MTF падает ниже 40%. Это означает хорошее воспроизведение контраста и среднюю степень детализации, которая проявляется в слабом эффекте размытия при большом увеличении картинки. Дальше от центра MTF при 10 л/мм падает до 70%, возрастает склонность к размытию при высоком контрасте границ. В углах изображения сагиттальные кривые тесно сближается при низком значении MTF поэтому следует ожидать значительного засвечивания углов открытыми источниками света.

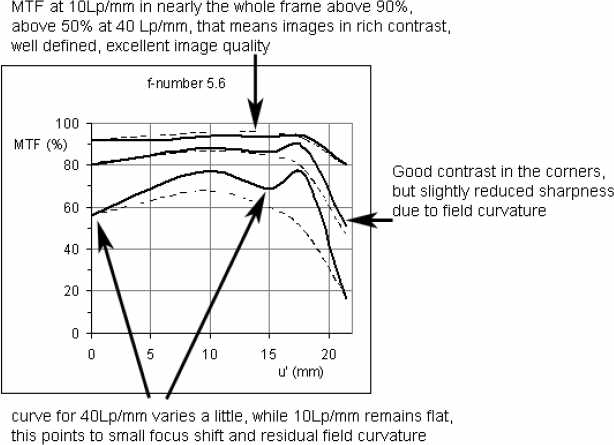
Если диафрагму прикрыть все показатели MTF сильно возрастают: кривые сближаются друг с другом и сильно поднимаются. Т.е. значения MTF снижаются относительно медленно с возрастанием пространственной частоты. Это означает отличное воспроизведение границ и очень хороший микроконтраст. В углу изображения все кривые несколько падают: для 10 л/мм немного, для более высоких частот – сильнее. Это указывает на хорошую плоскость поля зрения до, примерно, 18 мм высоты картинки, а затем о расфокусировке изображения в углах картинки из-за внезапно возникающей кривизны поля зрения. Не следует принимать слишком серьезно небольшие изменения кривой при 40 л/мм, они будут заметны лишь при очень большом увеличении картинки и когда фотографируют плоский объект; на большинстве изображений они просто не видны. Они вызваны кривизной поля зрения и сдвигом фокуса. Почему это происходит, мы узнаем в разделе о трехразмерных характеристиках MTF.

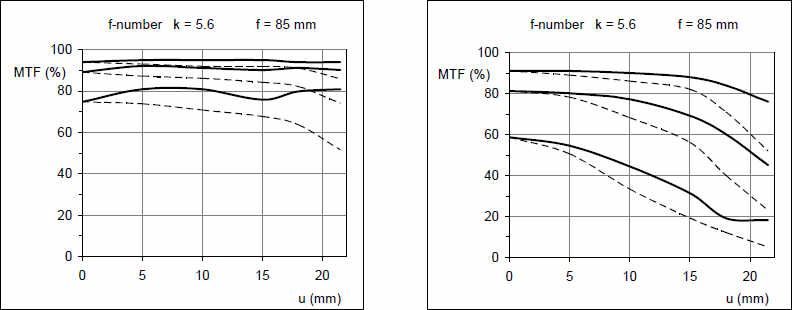
Сравнение двух объективов при одном фокусном расстоянии для 35 мм формата, на диафрагме 5,6. Слева высококачественный объектив (Planar 1.4/85 ZF), справа – недорогой 5-х зум объектив. Качество картинки первого по всему кадру ограничивается практически только свойствами сенсора и допускает самое большое увеличение. Зум-объектив достаточно хорош в центре, но значительно хуже у краев кадр. За исключением углов здесь можно ожидать хороший контраст, но у объектива отсутствует четкая резкость, т.к. MTF высоких частот падает быстрее. Изображения объектива могут быть рекомендованы только для небольшого увеличения.

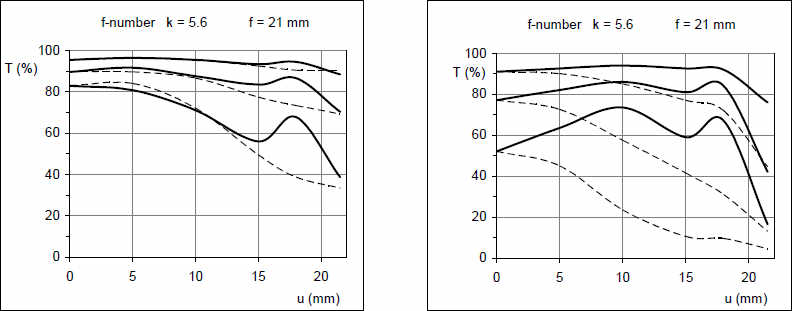
Сравнение двух широкоугольных объективов, которые значительно труднее в изготовлении, при диафрагме 5,6. Слева данные для Distagon 2.8/21 ZF, справа объектив, у которого боковые хроматические абберации устранены не так хорошо. У него объектив показывает некоторый сдвиг фокуса и, тем не менее, он не так и плох. Но тангенциальные MTF очень низки по краям кадра. Что это значит можно видеть на приведенных изображениях (200×200 пикс. с 12 МП картинки, высота изображения около 12 мм).

Трехразмерные характеристики

Очевидно, что разрешение картинки зависит от того, правильно ли была произведена фокусировка. Т.е. этот параметр можно описать кривой MTF. Сейчас мы познакомимся с мало известным типом кривых MTF. Этот показатель не является функцией частоты по высоте картинки, а описывает параметры фокуса. Для этого мы измеряем как MTF изменяется в продольном направлении плоскости изображения объектива и получили такие кривые:

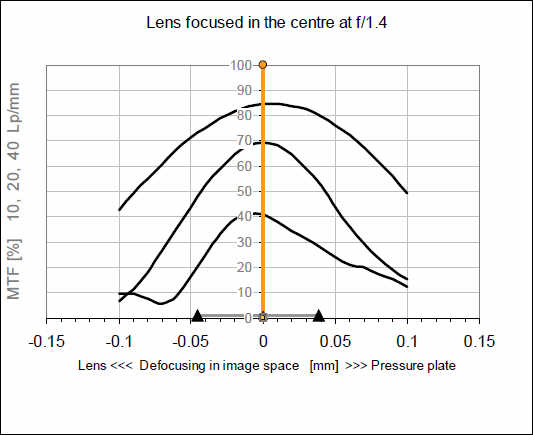
Значения MTF для 10, 20 и 40 л/мм вновь откладываются по вертикальной оси. Точка 0 на горизонтальной оси соответствует наилучшему фокусу; т.е. значение MTF для средней частоты — 20 л/мм здесь максимальна и именно здесь надо размещать сенсор или пленку, что обозначено желтой линией. Влево мы приближаемся к объективу, вправо мы отодвигаемся за сенсор.
Можно видеть, что приемлемые границы значения MTF для этой диафрагмы всего несколько сотых миллиметра. Два черных треугольничка показывают глубину фокусировки в плоскости изображения, подсчитанную чисто геометрически для круга смешения диаметром 0,03 мм. В соответствии с этим критерием, глубина области, находящейся в фокусе, ограничивается значением MTF равным 20% при 40 л/мм. Т.е. допускается, что максимальные значения для различных частот находятся в разных положениях, а кривые часто ассиметричны. Это означает, что тип размытия будет различным впереди и сзади фокуса. Что произойдет если уменьшить диафрагму? Мы уменьшили диафрагму на 3 ступени и повторили измерения, фокусировку не меняли, т.е. точка 0 все еще означает: MTF максимальна в центре картинки при 20 л/мм и диафрагме 1,4.

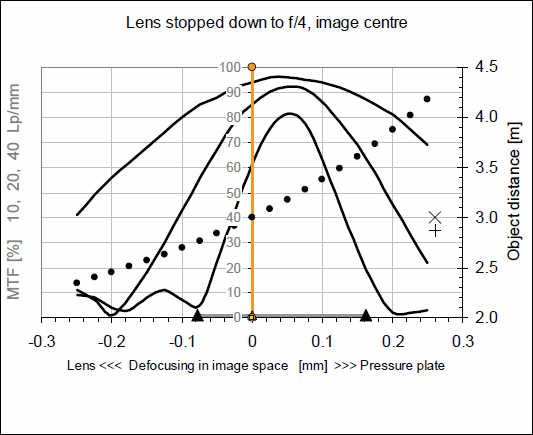
Максимальное значение MTF существенно возросло, т.к. снижение апертуры сильно снижает остаточную абберацию. В то же время мы отмечаем сдвиг всех кривых вправо, т.е. дальше от объектива. Объектив сейчас больше не фокусируется оптимально, т.е. в месте размещения сенсора (желтая линия), повышение MTF произошло, но не на этом месте. Геометрически рассчитанная глубина фокуса на плоскости изображения плохая, его длина вполне нормальная, а положение неверное. Такое явление называется «сдвиг фокуса», обычно оно свойственно объективам с большой апертурой и связано со сферической абберацией, что означает, что пучки света, проходящие через область диафрагмы на различном расстоянии от оптической оси, имеют разный фокус. В нашем случае сдвиг фокуса около 0,05 мм. Черные точки на вышеприведенном графике показывают, как этот сдвиг в пространстве изображения связан с расстоянием в пространстве объекта перед камерой (шкала с правой стороны графика). Если, например, первоначально при f/1,4 объектив был сфокусирован на расстояние 3 м, то сейчас, если другие настройки объектива не изменились, точка наилучшего фокуса сдвинулась на 3,25 м.
Следует ли вводить поправку на этот сдвиг фокуса при фотографировании? Вовсе нет, несмотря на то, что лучшее качество изображения в центре. 0,05 мм составляют около 20% расстояния между крайними точками глубины резкости для f/4 и поэтому трудно поддается точной корректировке. Кроме того, все равно в другой точке кадра картина будет совсем иной. Поэтому мы вновь измеряем MTF в продольном направлении, но не в центре, а на расстоянии 10 мм.

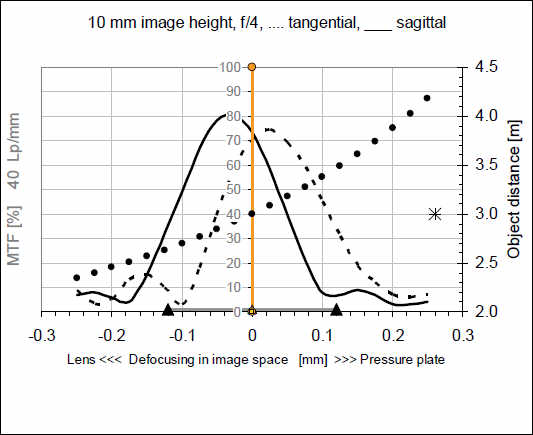
Здесь для наглядности мы приведем только тангенциальную и сагиттальную кривые для 40 л/мм, кривые для 10 и 20 л/мм не показаны. Мы видим, что обе кривые сдвинулись влево. Таким образом, положение максимума сдвигается, если мы перемещаемся по площади изображения.

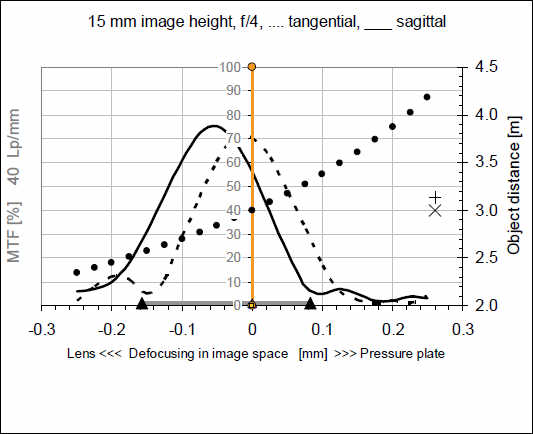
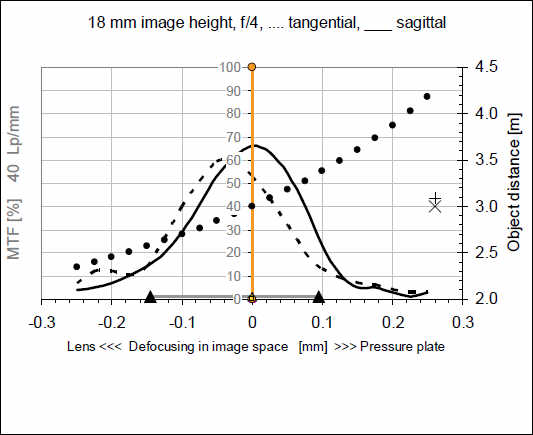
Здесь мы достигли края изображения на расстоянии 18 мм от центра и видно, что сагиттальная кривая возвращается к точке вблизи 0 нашей шкалы фокусировки. Т.е. по площади изображения кривая изменяется не единообразно, но могут быть и точки возврата. Комбинация остаточной кривизны плоскости и сдвиг фокуса приводят к тому, что MTF для объектива может выглядеть совершенно иначе, если мы не будем искать локальный максимум для каждой точки изображения, а будем регистрировать ее точно по плоскости изображения.

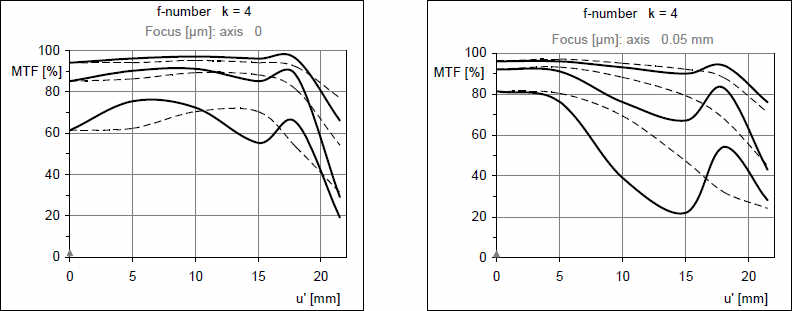
Потому эти два графика не означают: что левый объектив несколько хуже в центре, чем по полю, а правый объектив, напротив, отличный в центре, но в области дальше 15 мм имеет значительные нарушения. Оба графика получены на одном объективе, но с чуть разным фокусом. Отличия в 0,05 мм фокусировки того же порядка, как допуски обычной механической камеры, как установки АF на фокусировочном экране.

Пределы значимости кривых MTF

Явления, рассмотренные в предшествующей главе, являются удобным поводом поговорить об ограничениях этого мира цифр. Если форма кривой столь чувствительна к малейшим изменениям фокусировки, то, конечно, нельзя предсказать форму кривой для каждого изображения, если объект съемки трехмерный, т.е. когда изменение расстояния вызывает улучшение изображения одних деталей и ухудшение других. Условия измерения MTF можно сравнить с контактной печатью снимков, когда плоскость, в которой произведен один отпечаток, не отличается от плоскости, в которой произведен другой. Другим примером этого служат фотографии очень удаленного объекта, сделанные на коротком фокусном расстоянии.
Шкала измерения качества MTF не соответствует нашему восприятию. Требуется определенный опыт, для того чтобы, анализируя кривые MTF, предвидеть
субъективное восприятие изображения. Необходимо учитывать при этом и условия, в которых рассматривается изображение: рассматриваемое с одинакового расстояния, изображение в формате А4 будет значительно отличаться от такового на большом мониторе при 100% увеличении. Графически важная часть изображения обычно находится ниже кривой MTF для 40л/мм и выше кривой MTF для 10 л/мм. Почему же тогда количественную шкалу измерения MTF не подогнать под возможности нашего восприятия? Потому, что кривые MTF объективов характеризуют только первое звено в цепи формирования изображения и не принимают во внимание те, что следуют за ними. Сенсор, сканер, проектор, глаз, короче все последующее также всегда имеет свою функцию воспроизведения, которая снижается с увеличением пространственной частоты. И, т.о. приводит к ухудшению качества изображения объектива при высоких частотах, т.к. все функции воспроизведения перемножаются. Если, например, находиться сзади проектора, то глаз не сможет различить 40 л/мм.
Еще одной причиной является то, что во внимание не принимается логарифмическое восприятие яркости глазом. Проведено множество исследований, направленных на построение соответствия шкалы нашего восприятия и измерений MTF. Карл Цейс, например, пользуется числами Хейнахера (Heynacher numbers). Находят применение и другие психофизиологические факторы; н-р: SQF (subjective quality factor — субъективный количественный фактор), MTFA (modulation transfer area — область воспроизведения модуляции), SQRI (square root integral — сумма квадратных корней). Их общей чертой является то, что они подсчитывают площадь под кривой «модуляции предельной пространственной частоты». Общим у них является и то, что все они пытаются описать качество одной точки изображения одной цифрой. Выше мы уже видели, что иногда это приводит к неуместному упрощению данных.

Функция воспроизведения фазы

Желание упростить объясняет, почему до сих пор я не касался вопроса: как величина MTF соотносится с общими характеристиками корректированных объективов. Не секрет, что такую сложную систему как объектив нельзя описать несколькими цифрами. Описание изобразительных свойств объектива (компьютерное или лабораторное) занимает небольшую папку. Упрощение необходимо для того, чтобы сделать его понятным и ясным, при этом можно столкнуться с фактом, что четкость описания страдает.
Этого достаточно для введения, вернемся к деталям. Возможно, что два объектива, имеющие одинаковые MTF, формируют изображения заметно различающиеся в деталях. Например:

Детали края изображения, формируемые двумя короткофокусными светосильными объективами при полностью открытой диафрагме.

На картинке изображены крыша дома и дерево на фоне яркого неба, т.е. типичная картина горизонта с большим контрастом. MTF низкочастотных образцов важна, в частности, на границе темных объектов, т.к. она определяет степень засвечивания перехода к этим объектам. На левой картинке крыша не засвечивается, а дерево засвечивается. На правой картинке – наоборот. Если бы не дерево, то можно было бы считать, что левая картинка лучше (в черно-белом варианте, во всяком случае). Между тем, на этом расстоянии от центра кадра MTF обоих объективов одинаковы для всех пространственных частот. MTF ничего не говорит нам об этих различиях, т.к. не полностью описывает характеристики функции рассеяния точки. Действительно, полная функция оптического воспроизведения OTF (optical transfer function) – имеет вторую составляющую – функцию воспроизведения фазы – PTF (phase transfer function), которой обычно пренебрегают. Она в некоторой степени связана с симметрией функции рассеяния точки. Мы учитываем, что функция рассеяния точки может быть протяженной, иметь различные распределения в сагиттальном и тангенциальном направлениях. Поэтому мы измеряем по 2 MTF для каждой точки изображения. В предшествующих примерах мы мысленно предполагали, что распределения яркостей симметричны в каждом из перпендикулярных направлений функции рассеяния точки. На самом деле часто это не так. Функция рассеяния точки может быть ассиметричной, как это показано на следующем рисунке. Наиболее частой причиной этого являются запятовидные искажения, в результате которых функция рассеяния точки формируется с «хвостом» в радиальном направлении.

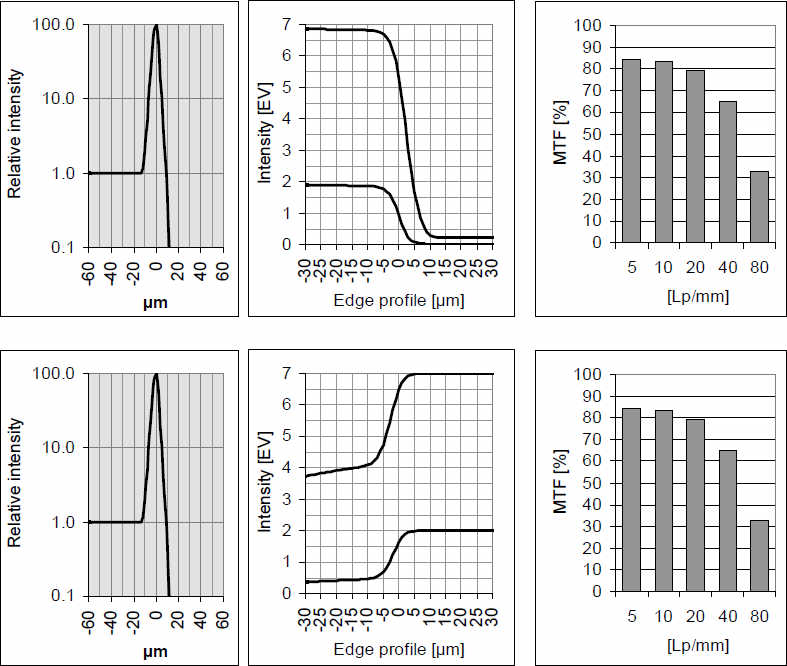
Для таких ассиметричных профилей яркости функции рассеяния точки ориентация границ в изображении, конечно, очень важна. Приведенная функция рассеяния точки слева имеет гало около 1% от максимальной яркости, справа она внезапно исчезает. Если яркая сторона границы в изображении будет справа, она будет давать подсветку влево (нижний рис.). Если же имеет место обратное, и левая сторона границы изображения яркая (верхн. рис.), тогда контраст на границе будет высокий, т.к. вправо функция рассеяние точки распространяется на очень короткое расстояние.
Величина MTF не учитывает этой зависимости от ориентации. Она учитывается функцией воспроизведения фазы, изменения которой зависят от ориентации «хвоста» функции рассеяния точки. Такое название происходит оттого, что такая ассиметричная функция рассеяния точки сдвигает фазу, т.е. положение ее максимума и минимума на синусоидальном образце.

Цветная коррекция

То, что оптические характеристики стекла зависят от длины волны света, можно также видеть на наших рисунках. Объективы имеют цветовые абберации. Хотя каждый объектив имеет подходящую систему компенсаций, использующую комбинацию различных типов стекла, приводящую к тому, что этот тип аббераций не представляет в настоящее время большой проблемы, некоторые остаточные абберации все-таки еще присутствуют. Есть объективы, где они более заметны, главным образом на длинном фокальном отрезке, где только сравнительно недавно удалось значительно улучшить качество изображения, благодаря появлению совершенно новых типов стекла. Длиннофокусные объективы, не обладающие линзами такого типа, т.е. с экстремально низкой дисперсией или аномальной остаточной дисперсией – достигают лишь посредственных величин MTF. Для многих объектов, тем не менее, с ними можно добиться очень хорошего качества изображения. Это происходит потому, что MTF таких объективов сильно зависит от спектрального состава света. Если произвести измерения с зеленым светом в сравнении с обычным белым, где в определенном соотношении присутствуют все длины волн видимого спектра, то кривые MTF будут разительно отличаться.

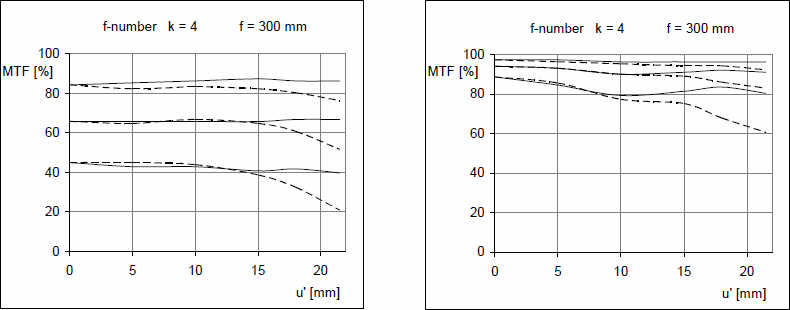
Кривые MTF длиннофокусного 300 мм объектива: слева измеренные в белом свете, справа в зеленом с длиной волны 100 нм

Именно поэтому зеленый фильтр был важной принадлежностью во времена черно-белой фотографии, Тот же эффект может быть достигнут в цветной фотографии, если объект съемки преимущественно одноцветный (фотографии природы, красных крыш).
Это еще одна причина, по которой свойства изображений не полностью отражаются с помощью кривых MTF.
Но не во всех случаях кривые MTF оценивают объективы так пессимистично. Напротив, возможно, когда недостаточная цветовая коррекция объектива не видна на MTF-данных для белого цвета. Другими словами: MTF мало говорит о цветной кайме. Сравнение MTF в белом и окрашенном свете помогает понять причины появления цветной каймы на изображении высококонтрастных переходов и светов. Следующие кривые иллюстрируют продольную хроматическую абберацию светосильного среднефокусного объектива путем измерения MTF как функции фокуса.

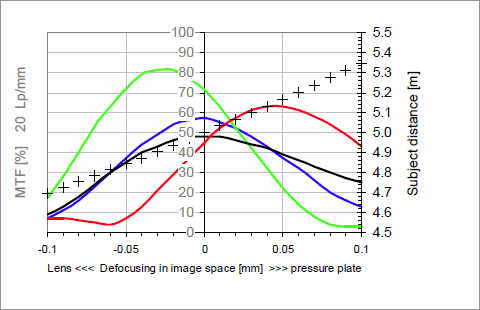
Фокусы MTF на полностью открытой диафрагме объектива Planar 1.4/85 ZA для белого (черная кривая), синего, зеленого и красного светов. Крестики связывают положение на стороне изображения (горизонтальная шкала) с расстоянием до объекта съемки (вертикальная правая шкала), объектив сфокусирован в белом свете на расстояние 5 м.

Значение MTF для окрашенных светов выше, чем для белого света, в тоже время их максимумы находятся в разных местах и не имеют единого фокуса. При лучшем фокусе для белого света ( положение 0) MTF для красного света вообще самая низкая. Из этого следует, что рассеяние красной линии имеет самый большой диаметр, а изображение, т.о. будет иметь слабую красноватую кайму. Это будет проявляться сильнее, если объект съемки будет находиться чуть ближе, там, где MTF зеленого света максимальна. Поэтому светосильные объективы такого типа дают кайму красного или пурпурного цвета на ярких деталях, если последние находятся перед плоскостью фокусировки и зеленую кайму — если за ней. Насыщенность этих цветов, называемых вторичным спектром, зависит от расстояния между пиками и пологости фокуса кривых MTF. Если у объективов имеются преимущественно монохроматические абберации (как у старых объективов), то кривые более плоские, а цвета тусклые. Современные хорошо откорректированные светосильные объективы склонны к образованию более насыщенных цветов. Поскольку расстояние между положениями пиков нельзя сделать неопределенно малым, единственным способом устранения каймы остается уменьшение диафрагмы. Глубина резкости при этом становится значительно больше, чем продольная хроматическая абберация, а различия MTF кривых окрашенных светов становятся малыми.

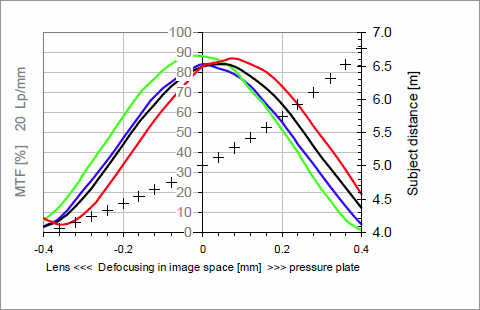
Фокусы MTF объектива Planar 1.4/85 ZA при f/5.6

Боке

Кривые, у которых величины тангенциального и сагиттального направлений близки по всему полю видимости часто называют идеальными кривыми MTF, т.к. в этих случаях «боке», т.е. изображение сильно расфокусированного заднего плана – особенно красивое.
Такие заявления следует принимать с осторожностью. MTF только дает представление о фокальной плоскости или ее непосредственном окружении. А в вышеупомянутом случае действительно преобладает округлая форма функции рассеяния точки, которая воспроизводит мелкие детали изображения настолько близко к оригиналу насколько это возможно, с наилучшим соответствием форме. Это важно для четкости письма, например.
Вместе с тем, невозможно использовать данные MTF для обоснования выводов о распределении яркости в пределах сильно расфокусированной точки рассеяния. Есть объективы с прекрасно параллельными тангенциальными и сагиттальными кривыми MTF, но которые сферически сильно перекорректированы. Это состояние коррекции вызывает кольцеобразную при расфокусировке функцию рассеяния точки, которая выглядит как круг света и как двойная линия, что дает беспокойно-выглядящий фон. Эту неприятную характеристику нельзя предсказать на основании кривых MTF.

Сравнимость данных MTF

Данные MTF публикуются во многих изданиях производителями объективов, а в настоящее время и независимыми испытателями. Несомненно, при сравнении этих данных следует быть осторожным, т.к. условия измерений могут сильно варьировать.
Наименее существенной и зачастую незамечаемой проблемой может быть разная частота образцов. Невозможность сравнения часто вызвана различной шириной спектра видимого света используемой в тестах.
Есть производители, которые не брезгуют публиковать данные, превышающие ограничения, накладываемые дифракцией, т.е. физически невозможные. Это говорит, что параметры получены просто путем расчета, и что в расчет принималась только геометрическая оптика, без учета волновых свойств света. Если такие объективы хорошо откорректированы, то значение MTF приближается к 100%. Но, пожалуйста, не верьте, что эти цифры реальны. Реальные объективы всегда немножко хуже, чем рассчитанные по программам проектирования оптики.
Величины MTF, публикуемые Zeiss, всегда основаны на результатах оценки объективов.